备考2024年中考数学探究性训练专题21 圆

更新时间：2024-03-31 浏览次数：36 类型：二轮复习

一、选择题

1. (2022·潍城模拟) “莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形，转子发动机的设计就是利用了莱洛三角形．它是分别以正三角形的顶点为圆心，以其边长为半径作弧形成的图形，如图2所示．若正三角形的边长为3，则该“莱洛三角形”的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·宾阳模拟) 如图，是古希腊数学家希波克拉底所研究的月牙问题，此图由三个半圆构成，三个半圆的直径分别为 $\text{[math]}$ 的三条边，若 $\text{[math]}$ ， $\text{[math]}$ ，则阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022九上·温州月考) 如图1，是清代数学家李之铉在他的著作《几何易简集》中研究过的一个图形，小圆同学在研究该图形后设计了图2，延长正方形 $\text{[math]}$ 的边 $\text{[math]}$ 至点 $\text{[math]}$ ，作矩形 $\text{[math]}$ ，以 $\text{[math]}$ 为直径作半圆 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边做正方形 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 上，记正方形 $\text{[math]}$ ，正方形 $\text{[math]}$ ，矩形 $\text{[math]}$ 的面积分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020九上·北京期中) 弧三角形，又叫莱洛三角形，是机械字家莱洛首先进行研究的.弧三角形是这样画的：先画正三角形，然后分别以三个顶点为圆心，（晓观数学）其边长为半径画弧得到的三角形.在大片的麦田或农田中，由农作物倒状形成的几何图案被称为“麦田怪圈”.图1中的麦田怪圈主要由圆和弧三角形构成，某研究小组根据照片尝试在操场上绘制类似的图形.如图2，成员甲先借绳子绕行一周画出 $\text{[math]}$ ，再将 $\text{[math]}$ 三等分，得到 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点.接着，成员乙分别以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为圆心画出图中的弧三角形.研究小组在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 四点中的某一点放置了检测仪器，记成员甲所在的位置为 $\text{[math]}$ ，成员乙所在的位置为 $\text{[math]}$ ，若将射线 $\text{[math]}$ 绕着点 $\text{[math]}$ 逆时针旋转到经过甲或乙的旋转角记为自变量 $\text{[math]}$ （单位：°， $\text{[math]}$ ），甲、乙两人到检测仪器的距离分别记为 $\text{[math]}$ 和 $\text{[math]}$ （单位： $\text{[math]}$ ），绘制出两个函数的图象（如图3）.
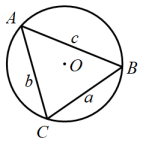
结合以上信息判断，下列说法中错误的是（）

A . $\text{[math]}$ 的半径为 $\text{[math]}$ B . 图3中 $\text{[math]}$ 的值为270 C . 当 $\text{[math]}$ 时， $\text{[math]}$ ₁取得最大值12 D . 检测仪器放置在点 $\text{[math]}$ 处

答案解析收藏纠错 + 选题

二、填空题

5. (2020·武汉模拟) （新知探究）新定义：平面内两定点 A， B ，所有满足 $\text{[math]}$ = k ( k 为定值)的 P 点形成的图形是圆，我们把这种圆称之为“阿氏圆”，
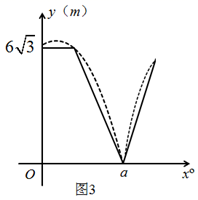
（问题解决）如图，在△ABC 中，CB = 4 ， AB= 2AC ，则△ABC 面积的最大值为.

答案解析收藏纠错 + 选题
6. (2013·成都) 如图，A，B，C为⊙O上相邻的三个n等分点， $\text{[math]}$ ，点E在 $\text{[math]}$ 上，EF为⊙O的直径，将⊙O沿EF折叠，使点A与A′重合，点B与B′重合，连接EB′，EC，EA′．设EB′=b，EC=c，EA′=p．现探究b，c，p三者的数量关系：发现当n=3时，p=b+c．请继续探究b，c，p三者的数量关系：当n=4时，p=；当n=12时，p=．
（参考数据：sin15°=cos75°= $\text{[math]}$ ，cos15°=sin75°= $\text{[math]}$ ）

答案解析收藏纠错 + 选题

三、理论探究题

7. (2024九下·阎良开学考) 【定义新知】
如图1， $\text{[math]}$ 是 $\text{[math]}$ 上两点，且在直径 $\text{[math]}$ 的上方，若直径 $\text{[math]}$ 上存在一点 $\text{[math]}$ ，连接 $\text{[math]}$ ，满足 $\text{[math]}$ ，则称 $\text{[math]}$ 是 $\text{[math]}$ 的“幸运角”．
1. （1）【问题探究】如图2， $\text{[math]}$ 是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 是 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
  ① $\text{[math]}$ 是 $\text{[math]}$ 的“幸运角”吗？请说明理由；
  ②设 $\text{[math]}$ 所对的圆心角为 $\text{[math]}$ ，请用含 $\text{[math]}$ 的式子表示 $\text{[math]}$ 的“幸运角”的度数；
2. （2）【拓展延伸】如图3，在（1）的条件下，若直径 $\text{[math]}$ ， $\text{[math]}$ 的“幸运角”为 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
8. (2024九上·长春汽车经济技术开发期末) 【问题呈现】小华在一次学习过程中遇到了下面的问题：

点 $\text{[math]}$ 为 $\text{[math]}$ 内一定点，点 $\text{[math]}$ 为 $\text{[math]}$ 上一动点，确定点 $\text{[math]}$ 的位置，使线段 $\text{[math]}$ 最长．
1. （1）【问题解决】以下是小华的方法：
  如图 $\text{[math]}$ ，连结 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 为所求．
  理由如下：在 $\text{[math]}$ 上取点 $\text{[math]}$ 异于点 $\text{[math]}$ ，连结 $\text{[math]}$ 、 $\text{[math]}$ ．
  接下来只需证明 $\text{[math]}$ ．
  请你补全小华的证明过程．
2. （2）【类比结论】点 $\text{[math]}$ 为 $\text{[math]}$ 外一定点，点 $\text{[math]}$ 为 $\text{[math]}$ 上一动点，设 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ 的长为 $\text{[math]}$ ，则线段 $\text{[math]}$ 长度的最大值为，线段 $\text{[math]}$ 长度的最小值为 $\text{[math]}$ 用含 $\text{[math]}$ 、 $\text{[math]}$ 的代数式表示 $\text{[math]}$
3. （3）【拓展延伸】如图 $\text{[math]}$ ，在半圆 $\text{[math]}$ 中，直径 $\text{[math]}$ 的长为 $\text{[math]}$ ，点 $\text{[math]}$ 在半圆 $\text{[math]}$ 上， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上运动，连结 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，连结 $\text{[math]}$ 在点 $\text{[math]}$ 运动的过程中，线段 $\text{[math]}$ 长度的最小值为．
答案解析收藏纠错 + 选题
9. (2024九上·湖南期末) 定义：当点P在射线OA上时，把 $\text{[math]}$ 的值叫做点P在射线OA上的射影值；当点P不在射线OA上时，把射线OA上与点P最近点的射影值，叫做点P在射线OA上的射影值．
例如：如图1，△OAB三个顶点均在格点上，BP是OA边上的高，则点P和点B在射线OA上的射影值均为 $\text{[math]}$ ．
1. （1）在△OAB中，
  ①点B在射线OA上的射影值小于1时，则△OAB是锐角三角形；
  ②点B在射线OA上的射影值等于1时，则△OAB是直角三角形；
  ③点B在射线OA上的射影值大于1时，则△OAB是钝角三角形．
  其中真命题有 ▲ ．
  $\text{[math]}$ ． ①② $\text{[math]}$ ． ①③ $\text{[math]}$ ． ②③ $\text{[math]}$ ． ①②③
2. （2）已知：点C是射线OA上一点，CA＝OA＝1，以〇为圆心，OA为半径画圆，点B是⊙O上任意点．
  ①如图2，若点B在射线OA上的射影值为 $\text{[math]}$ ．求证：直线BC是⊙O的切线；
  ②如图3，已知D为线段BC的中点，设点D在射线OA上的射影值为x ，点D在射线OB上的射影值为y ，直接写出y与x之间的函数关系式为．
答案解析收藏纠错 + 选题
10. (2023九上·南昌月考)
1. （1）知识重现：如图1，我们已经分三种情况探究了一条弧所对的圆周角 $\text{[math]}$ 和它所对的圆心角 $\text{[math]}$ 的数量关系．
  图1
  ①直接写出 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系 ▲ ．
  ②任选一种情况进行证明．
2. （2）迁移应用：如图2，已知 $\text{[math]}$ 内接于 $\text{[math]}$ ，直线DE是 $\text{[math]}$ 切线，切点为A，求证： $\text{[math]}$ ．
  图2
答案解析收藏纠错 + 选题
11. (2023九上·惠州月考) 综合探究
（一）新知学习：
人教版数学九年级上教材第119页《探究四点共圆的条件》发现，圆内接四边形的判断定理：如果四边形对角互补，那么这个四边新内接于圆（即如果四边形EFGH的对角互补，那么四边形 $\text{[math]}$ 的四个顶点E、F、G、H都在同个圆上）．
（二）问题解决：
已知 $\text{[math]}$ 的半径为2， $\text{[math]}$ 是 $\text{[math]}$ 的直径，P是 $\text{[math]}$ 上任意一点，过点P分别作 $\text{[math]}$ 的垂线，垂足分别为N ， M ．
1. （1）若直径 $\text{[math]}$ （如图1），在点P（不与B、C重合）从B运动到C的过程中， $\text{[math]}$ 的长是否为定值，若是，请并求出其定值；若不是，请说明理由．
2. （2）若直径 $\text{[math]}$ 与 $\text{[math]}$ 相交成 $\text{[math]}$ 角，当点P（不与B、C重合）从B点运动到C的过程中（如图2），证明 $\text{[math]}$ 的长为定值．
3. （3）试问当直径 $\text{[math]}$ 与 $\text{[math]}$ 相交成多少度角时， $\text{[math]}$ 的长取最大值，并写出其最大值．
答案解析收藏纠错 + 选题
12. (2023九上·杭州期中)
1. （1）【基础巩固】
  如图1，点A，F，B在同一直线上，若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）【尝试应用】
  如图2，AB是半圆 $\text{[math]}$ 的直径，弦长 $\text{[math]}$ 分别是AC，AB上的一点， $\text{[math]}$ ，若设 $\text{[math]}$ ，求出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系.
3. （3）【拓展提高】
  已知 $\text{[math]}$ 是等边 $\text{[math]}$ 边AB上的一点，现将 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 与 $\text{[math]}$ 重合，折痕为EF，点E，F分别在AC和BC上.如图3，如果 $\text{[math]}$ ，求CE：CF的值（用含n的代数式表示).
答案解析收藏纠错 + 选题
13. (2023九上·阿城期中) 先阅读材料，再解答问题：
小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图1，点A，B ， C，D均为 $\text{[math]}$ 上的点，则有 $\text{[math]}$ ．小明还发现，若点E在 $\text{[math]}$ 外，且与点D在直线 $\text{[math]}$ 同侧，则有 $\text{[math]}$ ．
请你参考小明得出的结论，解答下列问题：
问题：如图2，在平面直角坐标系 $\text{[math]}$ 中，点A的坐标为 $\text{[math]}$ ，点B的坐标为 $\text{[math]}$ ，点C的坐标为 $\text{[math]}$ ．
1. （1）在图2中作出 $\text{[math]}$ 的外接圆（保留必要的作图痕迹，不写作法），并求出此圆与x轴的另一个交点的坐标；
2. （2）点P为x轴正半轴上的一个动点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，当 $\text{[math]}$ 达到最大时，直接写出此时点P的坐标．
答案解析收藏纠错 + 选题
14. (2023九上·长春期中) 有关阿基米德折弦定理的探讨与应用
1. （1） [问题呈现]
  阿基术德折弦定理：如图①，AB和BC是⊙O的两条弦（即折线AB-BC是圆的一条折弦），BC> AB，点M是 $\text{[math]}$ 的中点，则从点M向BC作垂线，垂足D是折弦ABC的中点，即CD=DB+BA．
  下面是运用“截长法”证明CD=DB+BA的部分证明过程.
  证明：如图②，在CD上截取CE=AB，连接MA、MB、MC和ME.
  ∵M是 $\text{[math]}$ 的中点，∴MA=MC.
  ……
  请按照上面的证明思路，写出该证明的剩余部分.
2. （2） [理解运用]
  如图③，△ABC内接于⊙O，过点O作OD⊥AB于点D，延长DO交⊙O于点E，过点E作EF⊥AC于点F.若AC=10，BC=4，则CF的长为
3. （3） [实践应用]
  如图④，等边△ABC内接于⊙O，点D是 $\text{[math]}$ 上一点，且∠ABD= 45°，连接CD.若AB=2，则△BDC的周长为
答案解析收藏纠错 + 选题
15. 定义：两个角对应互余，且这两个角的夹边对应相等的两个三角形叫做“青竹三角形”.如图甲所示，在△ABC和△DEF中，若 $\text{[math]}$ $\text{[math]}$ ，且 $\text{[math]}$ ，则△ABC和DEF是“青竹三角形”.
1. （1）下列四边形中，一定能被一条对角线分成两个“青竹三角形”的是.(填序号)
  ①平行四边形②矩形③菱形④正方形
2. （2）如图乙所示，在△ABC中， $\text{[math]}$ ，点 $\text{[math]}$ 是AB上任意一点（不与点A，B重合），设AD，BD，CD的长分别为a，b，c，请写出图中的一对“青竹三角形”，并用含a，b的式子来表示 $\text{[math]}$ .
3. （3）如图丙所示， $\text{[math]}$ 的半径为4，四边形ABCD是 $\text{[math]}$ 的内接四边形，且 $\text{[math]}$ 和 $\text{[math]}$ 是“青竹三角形”.
  ①求 $\text{[math]}$ 的值；
  ②若 $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的周长之差.
答案解析收藏纠错 + 选题
16. (2023九上·拱墅开学考) 若凸四边形的两条对角线所夹锐角为 $\text{[math]}$ ，我们称这样的凸四边形为“美丽四边形”．
1. （1） ①在“平行四边形、矩形、菱形、正方形”中，一定不是“美丽四边形”的有；
  ②若矩形 $\text{[math]}$ 是“美丽四边形”，且 $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）如图 $\text{[math]}$ ， “美丽四边形” $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，且对角线 $\text{[math]}$ ，为直径， $\text{[math]}$ ， $\text{[math]}$ ，求另一条对角线 $\text{[math]}$ 的长；
3. （3）如图 $\text{[math]}$ ，平面直角坐标系中，已知“美丽四边形” $\text{[math]}$ 的四个顶点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在第三象限， $\text{[math]}$ 在第一象限， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，且四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，若二次函数 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为常数，且 $\text{[math]}$ 的图象同时经过这四个顶点，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
17. (2023·长春)
1. （1）【感知】如图①，点A、B、P均在 $\text{[math]}$ 上， $\text{[math]}$ ，则锐角 $\text{[math]}$ 的大小为度．
2. （2）【探究】小明遇到这样一个问题：如图②， $\text{[math]}$ 是等边三角形 $\text{[math]}$ 的外接圆，点P在 $\text{[math]}$ 上（点P不与点A、C重合），连结 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ．求证： $\text{[math]}$ ．小明发现，延长 $\text{[math]}$ 至点E，使 $\text{[math]}$ ，连结 $\text{[math]}$ ，通过证明 $\text{[math]}$ ，可推得 $\text{[math]}$ 是等边三角形，进而得证．
  下面是小明的部分证明过程：
  证明：延长 $\text{[math]}$ 至点E，使 $\text{[math]}$ ，连结 $\text{[math]}$ ，
        $\text{[math]}$ 四边形 $\text{[math]}$ 是 $\text{[math]}$ 的内接四边形，
        $\text{[math]}$ ．
        $\text{[math]}$ ，
        $\text{[math]}$ ．
        $\text{[math]}$ 是等边三角形．
        $\text{[math]}$ ，
        $\text{[math]}$
  请你补全余下的证明过程．
3. （3）【应用】如图③， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ ，点P在 $\text{[math]}$ 上，且点P与点B在 $\text{[math]}$ 的两侧，连结 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．
答案解析收藏纠错 + 选题
18. (2023九下·杭州月考)
1. （1）【证明体验】
  如图1，⊙O是等腰△ABC的外接圆，AB＝AC ，在 $\text{[math]}$ 上取一点P ，连结AP ， BP ， CP ．求证：∠APB＝∠PAC+∠PCA；
2. （2）【思考探究】
  如图2，在（1）条件下，若点P为 $\text{[math]}$ 的中点，AB＝6，PB＝5，求PA的值；
3. （3）【拓展延伸】
  如图3，⊙O的半径为5，弦BC＝6，弦CP＝5，延长AP交BC的延长线于点E ，且∠ABP＝∠E ，求AP•PE的值．
答案解析收藏纠错 + 选题
19. (2022·宿迁) 如图，在网格中，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 均为格点.
1. （1）【操作探究】在数学活动课上，佳佳同学在如图①的网格中，用无刻度的直尺画了两条互相垂直的线段 $\text{[math]}$ 、 $\text{[math]}$ ，相交于点 $\text{[math]}$ 并给出部分说理过程，请你补充完整：
  
  解：在网格中取格点 $\text{[math]}$ ，构建两个直角三角形，分别是△ABC和△CDE.
  
  在Rt△ABC中， $\text{[math]}$
  
  在Rt△CDE中，，
  
  所以 $\text{[math]}$ .
  
  所以∠ $\text{[math]}$ =∠ $\text{[math]}$ .
  
  因为∠ $\text{[math]}$ ∠ $\text{[math]}$ =∠ $\text{[math]}$ =90°，
  
  所以∠ $\text{[math]}$ +∠ $\text{[math]}$ =90°，
  
  所以∠ $\text{[math]}$ =90°，
  
  即 $\text{[math]}$ ⊥ $\text{[math]}$ .
2. （2）【拓展应用】如图②是以格点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为直径的圆，请你只用无刻度的直尺，在 $\text{[math]}$ 上找出一点P，使 $\text{[math]}$ ，写出作法，并给出证明：
3. （3）【拓展应用】如图③是以格点 $\text{[math]}$ 为圆心的圆，请你只用无刻度的直尺，在弦 $\text{[math]}$ 上找出一点P.使 $\text{[math]}$ = $\text{[math]}$ · $\text{[math]}$ ，写出作法，不用证明.
答案解析收藏纠错 + 选题
20. (2022·清苑模拟) 【问题提出】
如图1， $\text{[math]}$ 与直线 $\text{[math]}$ 相离，过圆心 $\text{[math]}$ 作直线 $\text{[math]}$ 的垂线，垂足为 $\text{[math]}$ ，且交 $\text{[math]}$ 于 $\text{[math]}$ 、 $\text{[math]}$ 两点（ $\text{[math]}$ 在 $\text{[math]}$ 、 $\text{[math]}$ 之间）．我们把点 $\text{[math]}$ 称为 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“远点”，把 $\text{[math]}$ 的值称为 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“远望数”．
1. （1）如图2，在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，过点 $\text{[math]}$ 画垂直于 $\text{[math]}$ 轴的直线 $\text{[math]}$ ，则半径为1的 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“远点”坐标是，直线 $\text{[math]}$ 向下平移个单位长度后与 $\text{[math]}$ 相切．
2. （2）在（1）的条件下求 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“远望数”．
3. （3）【拓展应用】
  如图3，在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作 $\text{[math]}$ ．若 $\text{[math]}$ 与直线 $\text{[math]}$ 相离， $\text{[math]}$ 是 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“远点”．且 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“远望数”是 $\text{[math]}$ ，求直线 $\text{[math]}$ 的函数表达式．
答案解析收藏纠错 + 选题
21. (2022·泗水模拟) 阅读资料：如图1，在平面之间坐标系 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 两点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，由勾股定理得 $\text{[math]}$ ，所以 $\text{[math]}$ ， $\text{[math]}$ 两点间的距离为 $\text{[math]}$ ．我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 为圆上任意一点，则 $\text{[math]}$ 到原点的距离的平方为 $\text{[math]}$ ，当 $\text{[math]}$ 的半径为 $\text{[math]}$ 时， $\text{[math]}$ 的方程可写为： $\text{[math]}$ ．
问题拓展：如果圆心坐标为 $\text{[math]}$ ，半径为 $\text{[math]}$ ，那么 $\text{[math]}$ 的方程可以写为 $\text{[math]}$ ．

综合应用：如图3， $\text{[math]}$ 与 $\text{[math]}$ 轴相切于原点 $\text{[math]}$ ， $\text{[math]}$ 点坐标为 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，使 $\text{[math]}$ ，作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证 $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）是否存在到四点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 距离都相等的点 $\text{[math]}$ ？若存在，求 $\text{[math]}$ 点坐标，并写出以 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 为半径的 $\text{[math]}$ 的方程；若不存在，说明理由．
答案解析收藏纠错 + 选题
22. (2021·北仑模拟) 如图
1. （1）【根底巩固】
  如图，在 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 上一点， $\text{[math]}$ . 求证： $\text{[math]}$ .
2. （2）【尝试应用】
  如图2，在菱形 $\text{[math]}$ 中， $\text{[math]}$ 分别为 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，射线 $\text{[math]}$ 交 $\text{[math]}$ 的延长线与点 $\text{[math]}$ ，射线 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ . 若 $\text{[math]}$ . $\text{[math]}$ .
  
  求： ①CM的长；
  
  ②FN的长.
3. （3）【拓展进步】
  如图3，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心作半径为3的圆，其中点 $\text{[math]}$ 是圆上的动点，请直接写出 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
23. (2022九上·奉化期末) 阅读材料，某个学习小组成员发现：在等腰 $\text{[math]}$ 中，AD平分 $\text{[math]}$ ， ∵ $\text{[math]}$ ， $\text{[math]}$ ， ∴ $\text{[math]}$ ，他们猜想：在任意 $\text{[math]}$ 中，一个内角角平分线分对边所成的两条线段与这个内角的两边对应成比例.
【证明猜想】如图1所示，在 $\text{[math]}$ 中，AD平分 $\text{[math]}$ ，求证： $\text{[math]}$ .
丹丹认为，可以通过构造相似三角形的方法来证明；
思思认为，可以通过比较 $\text{[math]}$ 和 $\text{[math]}$ 面积的角度来证明.
1. （1）请你从上面的方法中选择一种进行证明.
2. （2）【尝试应用】如图2， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆，点E是 $\text{[math]}$ 上一点（与B不重合，且 $\text{[math]}$ ，连结 $\text{[math]}$ ，并延长AE，BC交于点D，H为AE的中点，连结BH交AC于点G，求 $\text{[math]}$ 的值.
3. （3）【拓展提高】如图3，在（2）的条件下，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点F，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的直径（用x的代数式表示）.
答案解析收藏纠错 + 选题

24. (2021·息县模拟) 请阅读材料，并完成相应的任务.

在数学探究课上，同学们在探索与圆有关的角的过程中发现这些角的两边都与圆相交，不断改变顶点的位置，可形成无数个角，而根据点和圆的位置关系可将这些角分为三类，分别是顶点在圆上、圆外和圆内的角结合教学课上学习的圆周角的概念，对顶点在圆外和圆内的角进行定义：顶点在圆外，两边与圆相交的角叫做圆外角.顶点在圆内，两边都与圆相交的角叫做圆内角，如图1， $\text{[math]}$ 和 $\text{[math]}$ 分别是 $\text{[math]}$ 所对的圆外角和圆内角.

如图2，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 为 $\text{[math]}$ 所对的一个圆外角. $\text{[math]}$ 分别交 $\text{[math]}$ 于点 $\text{[math]}$ .若 $\text{[math]}$ 所对的圆心角为 $\text{[math]}$ ，求 $\text{[math]}$ .勤奋小组的解题过程（部分）如下：

解：如图2，连接 $\text{[math]}$ .

$\text{[math]}$ 是 $\text{[math]}$ 所对的圆周角，且 $\text{[math]}$ ，

$\text{[math]}$ .

…

任务：

（1）如图1，在探究与圆有关的角时，运用的数学思想方法是：____；

A . 公理化思想 B . 分类讨论 C . 数形结合
（2）将勤奋小组的解题过程补充完整；
（3）如图3，当点 $\text{[math]}$ 在 $\text{[math]}$ 内时， $\text{[math]}$ 是 $\text{[math]}$ 所对的一个圆内角，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若设 $\text{[math]}$ 所对的圆心角为 $\text{[math]}$ ，则 $\text{[math]}$ °.

答案解析收藏纠错 + 选题

四、实践探究题

25. (2023九上·深圳期中) 小学阶段，我们了解到圆：平面上到定点的距离等于定长的所有的点组成的图形叫做圆。在一节数学实践活动课上，老师手拿着三个正方形硬纸板和几个不同的圆形的盘子，他向同学们提出了这样一个问题：已知手中圆盘的直径为 $\text{[math]}$ ，手中的三个正方形硬纸板的边长均为 $\text{[math]}$ ，若将三个正方形纸板不重叠地放在桌面上，能否用这个圆盘将其盖住？问题提出后，同学们七嘴八舌，经过讨论，大家得出了一致性的结论是：本题实际上是求在不同情况下将三个正方形硬纸板无重叠地适当放置，圆盘能盖住时的最小直径.然后将各种情形下的直径值与 $\text{[math]}$ 进行比较，若小于或等于 $\text{[math]}$ 就能盖住，反之，则不能盖住.老师把同学们探索性画出的四类图形画在黑板上，如图所示.
1. （1）通过计算，在图1中圆盘刚好能盖住正方形纸板的最小直径应为 $\text{[math]}$ .（填准确数
2. （2）图2能盖住三个正方形硬纸板所需的圆盘最小直径为 $\text{[math]}$ ，图3能盖住三个正方形硬纸板所需的圆盘最小直径为 $\text{[math]}$ .（填准确数）
3. （3）拓展：按图4中的放置，三个正方形放置后为轴对称图形，当圆心 $\text{[math]}$ 落在 $\text{[math]}$ 边上时，圆的直径是多少，请你写出该种情况下求圆盘最小直径的过程，并判断是否能盖住.（计算中可能用到的数据，为了计算方便，本问在计算过程中，根据实际情况最后的结果可对个别数据取整数）
答案解析收藏纠错 + 选题
26. (2024九下·深圳开学考) 综合与实践
数学活动课上，老师出示了一个问题：如图，已知三只蚂蚁A、 $\text{[math]}$ 、 $\text{[math]}$ 在半径为 $\text{[math]}$ 的 $\text{[math]}$ 上静止不动，第四只蚂蚁 $\text{[math]}$ 在 $\text{[math]}$ 上的移动，并始终保持 $\text{[math]}$ ．
1. （1）请判断 $\text{[math]}$ 的形状；“数学希望小组”很快得出结论，请你回答这个结论： $\text{[math]}$ 是三角形；
2. （2） “数学智慧小组”继续研究发现：当第四只蚂蚁 $\text{[math]}$ 在 $\text{[math]}$ 上的移动时，线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三者之间存在一种数量关系：请你写出这种数量关系： ▲ ，并加以证明；
3. （3） “数学攀峰小组”突发奇想，深入探究发现：若第五只蚂蚁 $\text{[math]}$ 同时随着蚂蚁 $\text{[math]}$ 的移动而移动，且始终位于线段 $\text{[math]}$ 的中点，在这个运动过程中，线段 $\text{[math]}$ 的长度一定存在最小值，请你求出线段 $\text{[math]}$ 的最小值是（不写解答过程，直接写出结果）．
答案解析收藏纠错 + 选题
27. (2023·潍坊模拟) 【定义】从一个已知图形的外一点引两条射线分别经过该已知图形的两点，则这两条射线所成的最大角称为该点对已知图形的视角，如图①， $\text{[math]}$ 是点P对线段 $\text{[math]}$ 的视角．
1. （1）【应用】
  如图②，在直角坐标系中，已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则原点O对三角形 $\text{[math]}$ 的视角为；
2. （2）如图③，在直角坐标系中，以原点O，半径为2画圆 $\text{[math]}$ ，以原点O，半径为4画圆 $\text{[math]}$ ，证明：圆 $\text{[math]}$ 上任意一点P对圆 $\text{[math]}$ 的视角是定值；
3. （3）【拓展应用】
  很多摄影爱好者喜欢在天桥上对城市的标志性建筑拍照，如图④．现在有一条笔直的天桥，标志性建筑外延呈正方形，摄影师想在天桥上找到对建筑视角为 $\text{[math]}$ 的位置拍摄．现以建筑的中心为原点建立如图⑤的坐标系，此时天桥所在的直线的表达式为 $\text{[math]}$ ，正方形建筑的边长为4，请直接写出直线上满足条件的位置坐标．
答案解析收藏纠错 + 选题
28. (2023·香洲模拟) 小辉同学观看2022卡塔尔世界杯时发现，优秀的球员通常都能选择最优的点射门（仅从射门角度大小考虑）．这引起了小辉同学的兴趣，于是他展开了一次有趣的数学探究．

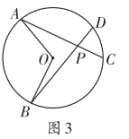
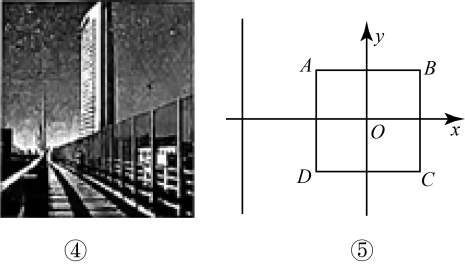
【提出问题】如图所示．球员带球沿直线 $\text{[math]}$ 奔向球门 $\text{[math]}$ ，

探究：是否存在一个位置，使得射门角度最大．

【分析问题】因为线段 $\text{[math]}$ 长度不变，我们联想到圆中的弦和圆周角．

如图1，射线 $\text{[math]}$ 与 $\text{[math]}$ 相交，点M，点A，点N分别在圆外、圆上、圆内，连接 $\text{[math]}$ ．

【解决问题】
1. （1）如图1，比较 $\text{[math]}$ 的大小：（用“<”连接起来）．
2. （2）如图2，点A是射线 $\text{[math]}$ 上一动点（点A不与点B重合）．证明：当 $\text{[math]}$ 的外接圆 $\text{[math]}$ 与射线 $\text{[math]}$ 相切时， $\text{[math]}$ 最大．
3. （3）【延伸拓展】在（2）的条件下，如果 $\text{[math]}$ ．当 $\text{[math]}$ 最大时．证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
29. (2022九上·寒亭期中) 【阅读理解】：如图，在 $\text{[math]}$ 中，a，b，c分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边， $\text{[math]}$ ，其外接圆半径为R．根据锐角三角函数的定义： $\text{[math]}$ ， $\text{[math]}$ ，可得 $\text{[math]}$ ，即 $\text{[math]}$ （规定 $\text{[math]}$ ）．
1. （1）【探究活动】：如图，在锐角 $\text{[math]}$ 中，a，b，c分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边，其外接圆半径为R，那么： $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ （用>，=或<连接），并说明理由．
2. （2）【初步应用】：事实上，以上结论适用于任意三角形．在 $\text{[math]}$ 中，a，b，c分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边．已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ．
3. （3）【综合应用】：如图，在某次数学实践活动中，小莹同学测量一栋楼 $\text{[math]}$ 的高度，在A处用测角仪测得地面点C处的俯角为45°，点D处的俯角为15°，B，C，D在一条直线上，且C，D两点的距离为100m，求楼 $\text{[math]}$ 的高度．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
30. (2023·苍溪模拟) 【问题探究】
1. （1）如图1，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 于点F， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点N，则 $\text{[math]}$ 的长为；
2. （2）如图2，点M是正方形 $\text{[math]}$ 对角线 $\text{[math]}$ 上的动点，连接 $\text{[math]}$ 于点H，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，在M点从C到A的运动过程中，求 $\text{[math]}$ 的最小值；
3. （3）【问题解决】
  如图3，某市欲规划一块形如矩形 $\text{[math]}$ 的休闲旅游观光区，其中 $\text{[math]}$ 米， $\text{[math]}$ 米，点E、F是观光区的两个入口（点E、F分别为 $\text{[math]}$ 的中点），P，Q分别在线段 $\text{[math]}$ 上，设计者欲从P到Q修建绿化带 $\text{[math]}$ ，从B到H修建绿化带 $\text{[math]}$ ，绿化带宽度忽略不计，且满足 $\text{[math]}$ ，点H在 $\text{[math]}$ 上， $\text{[math]}$ ．为了方便市民游览，计划从D到H修建观光通道 $\text{[math]}$ ，根据设计要求，请你帮助设计者求出观光通道 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题