全国历年中考数学真题精选汇编：圆2

更新时间：2021-07-09 浏览次数：110 类型：二轮复习

一、填空题

1. (2020·连云港) 如图，正六边形 $\text{[math]}$ 内部有一个正五形 $\text{[math]}$ ，且 $\text{[math]}$ ，直线 $\text{[math]}$ 经过 $\text{[math]}$ 、 $\text{[math]}$ ，则直线 $\text{[math]}$ 与 $\text{[math]}$ 的夹角 $\text{[math]}$ $\text{[math]}$ .

答案解析收藏纠错 + 选题
2. (2018·眉山) 如图，△ABC是等腰直角三角形，∠ACB=90°，AC=BC=2，把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是.

答案解析收藏纠错 + 选题

二、综合题

3. (2021·长沙) 如图，点 $\text{[math]}$ 为以 $\text{[math]}$ 为直径的半圆的圆心，点 $\text{[math]}$ ， $\text{[math]}$ 在直径 $\text{[math]}$ 上，点 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 上，四边形 $\text{[math]}$ 为正方形，点 $\text{[math]}$ 在 $\text{[math]}$ 上运动（点 $\text{[math]}$ 与点 $\text{[math]}$ ， $\text{[math]}$ 不重合），连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的值；
2. （2）求 $\text{[math]}$ 的值；
3. （3）令 $\text{[math]}$ ， $\text{[math]}$ ，直径 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 是常数），求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式，并指明自变量 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
4. (2021·自贡) 如图，点D在以AB为直径的⊙O上，过D作⊙O的切线交AB延长线于点C，AE⊥CD于点E，交⊙O于点F，连接AD，FD.
1. （1）求证：∠DAE＝∠DAC；
2. （2）求证：DF•AC＝AD•DC；
3. （3）若sin∠C＝ $\text{[math]}$ ，AD＝4 $\text{[math]}$ ，求EF的长.
答案解析收藏纠错 + 选题
5. (2020·锦州) 如图， $\text{[math]}$ 的对角线 $\text{[math]}$ 交于点E，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 经过点E，与 $\text{[math]}$ 交于点F，G是 $\text{[math]}$ 延长线上一点，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点H，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的直径.
答案解析收藏纠错 + 选题
6. (2020·鄂尔多斯) 我们知道，顶点坐标为(h，k)的抛物线的解析式为y＝a（x﹣h）²+k（a≠0）．今后我们还会学到，圆心坐标为(a，b)，半径为r的圆的方程（x﹣a）²+（y﹣b）²＝r² ，如：圆心为P(﹣2，1)，半径为3的圆的方程为（x+2）²+（y﹣1）²＝9．
1. （1）以M(﹣3，﹣1)为圆心， $\text{[math]}$ 为半径的圆的方程为．
2. （2）如图，以B(﹣3，0)为圆心的圆与y轴相切于原点，C是⊙B上一点，连接OC，作BD⊥OC，垂足为D，延长BD交y轴于点E，已知sin∠AOC＝ $\text{[math]}$ ．
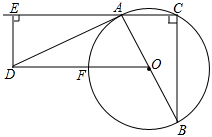
  ①连接EC，证明：EC是⊙B的切线；
  
  ②在BE上是否存在一点Q，使QB＝QC＝QE＝QO？若存在，求点Q的坐标，并写出以Q为圆心，以QB为半径的⊙Q的方程；若不存在，请说明理由．
答案解析收藏纠错 + 选题
7. (2020·黔南) 如图，已知AB是⊙O的直径，⊙O经过Rt△ACD的直角边DC上的点F，交AC边于点E，点F是弧EB的中点，∠C＝90°，连接AF.
1. （1）求证：直线CD是⊙O切线.
2. （2）若BD＝2，OB＝4，求tan∠AFC的值.
答案解析收藏纠错 + 选题
8. (2020·黔南) 古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的圆”，请研究如下美丽的圆，如图，Rt△ABC中，∠BCA＝90°，AC＝3，BC＝4，点O在线段BC上，且OC＝ $\text{[math]}$ ，以O为圆心.OC为半径的⊙O交线段AO于点D，交线段AO的延长线于点E.
1. （1）求证：AB是⊙O的切线；
2. （2）研究过短中，小明同学发现 $\text{[math]}$ ＝ $\text{[math]}$ ，回答小明同学发现的结论是否正确？如果正确，给出证明；如果不正确，说明理由.
答案解析收藏纠错 + 选题
9. (2020·襄阳) 如图， $\text{[math]}$ 是⊙O的直径，E，C是 $\text{[math]}$ 上两点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，过点C作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点D.
1. （1）判定直线 $\text{[math]}$ 与⊙O的位置关系，并说明理由；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求图中阴影部分的面积.
答案解析收藏纠错 + 选题
10. (2020·鄂州) 如图所示： $\text{[math]}$ 与 $\text{[math]}$ 的边 $\text{[math]}$ 相切于点C，与 $\text{[math]}$ 、 $\text{[math]}$ 分别交于点D、E， $\text{[math]}$ . $\text{[math]}$ 是 $\text{[math]}$ 的直径.连接 $\text{[math]}$ ，过C作 $\text{[math]}$ 交 $\text{[math]}$ 于G，连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点F.
1. （1）求证：直线 $\text{[math]}$ 与 $\text{[math]}$ 相切；
2. （2）求证： $\text{[math]}$ ；
3. （3）若 $\text{[math]}$ 时，过A作 $\text{[math]}$ 交 $\text{[math]}$ 于M、N两点（M在线段 $\text{[math]}$ 上），求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
11. (2020·常州) 如图1，⊙I与直线a相离，过圆心I作直线a的垂线，垂足为H，且交⊙I于P、Q两点（Q在P、H之间）.我们把点P称为⊙I关于直线a的“远点”，把 $\text{[math]}$ 的值称为⊙I关于直线a的“特征数”.
1. （1）如图2，在平面直角坐标系 $\text{[math]}$ 中，点E的坐标为 $\text{[math]}$ ，半径为1的⊙O与两坐标轴交于点A、B、C、D.
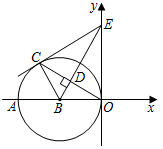
  ①过点E画垂直于y轴的直线m，则⊙O关于直线m的“远点”是点_▲__（填“A”、“B”、“C”或“D”），⊙O关于直线m的“特征数”为_▲__；
  
  ②若直线n的函数表达式为 $\text{[math]}$ ，求 $\text{[math]}$ 关于直线n的“特征数”；
2. （2）在平面直角坐标系 $\text{[math]}$ 中，直线l经过点 $\text{[math]}$ ，点F是坐标平面内一点，以F为圆心， $\text{[math]}$ 为半径作⊙F.若⊙F与直线l相离，点 $\text{[math]}$ 是⊙F关于直线l的“远点”，且⊙F关于直线l的“特征数”是 $\text{[math]}$ ，求直线l的函数表达式.
答案解析收藏纠错 + 选题
12. (2020·孝感) 已知 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平分线与 $\text{[math]}$ 交于点D，与 $\text{[math]}$ 交于点E，连接 $\text{[math]}$ 并延长与 $\text{[math]}$ 过点A的切线交于点F，记 $\text{[math]}$ .
1. （1）如图1，若 $\text{[math]}$ ，
  ①直接写出 $\text{[math]}$ 的值为；
  
  ②当 $\text{[math]}$ 的半径为2时，直接写出图中阴影部分的面积为；
2. （2）如图2，若 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
13. (2020·咸宁) 定义：有一组对角互余的四边形叫做对余四边形.
1. （1）理解：若四边形 $\text{[math]}$ 是对余四边形，则 $\text{[math]}$ 与 $\text{[math]}$ 的度数之和为；
2. （2）证明：如图1， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ 相交于点D.
  求证：四边形 $\text{[math]}$ 是对余四边形；
3. （3）探究：如图2，在对余四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，探究线段 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 之间有怎样的数量关系？写出猜想，并说明理由.
答案解析收藏纠错 + 选题
14. (2020·武汉) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的⊙O交 $\text{[math]}$ 于点D， $\text{[math]}$ 与过点D的切线互相垂直，垂足为E.
1. （1）求证： $\text{[math]}$ 平分 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
15. (2020·恩施) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，直线 $\text{[math]}$ 与 $\text{[math]}$ 相切于点A，直线 $\text{[math]}$ 与 $\text{[math]}$ 相切于点B，点C（异于点A）在 $\text{[math]}$ 上，点D在 $\text{[math]}$ 上，且 $\text{[math]}$ ，延长 $\text{[math]}$ 与 $\text{[math]}$ 相交于点E，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点F.
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）求证： $\text{[math]}$ ；
3. （3）如图，连接 $\text{[math]}$ 并延长与 $\text{[math]}$ 分别相交于点G、H，连接 $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
16. (2020·新疆) 如图，在⊙O中，AB为⊙O的直径，C为⊙O上一点，P是 $\text{[math]}$ 的中点，过点P作AC的垂线，交AC的延长线于点D.
1. （1）求证：DP是⊙O的切线；
2. （2）若AC=5，sin∠APC= $\text{[math]}$ ，求AP的长.
答案解析收藏纠错 + 选题
17. (2020·杭州) 如图，已知AC，BD为⊙O的两条直径，连接AB，BC，OE⊥AB于点E，点F是半径OC的中点，连接EF.
1. （1）设⊙O的半径为1，若∠BAC=30°，求线段EF的长。
2. （2）连接BF，DF
  ①求证：PE=PF
  
  ②若DF=EF，求∠BAC的度数。
答案解析收藏纠错 + 选题
18. (2019·杭州) 如图，已知锐角三角形ABC内接于⊙O，OD⊥BC于点D，连接OA.
1. （1）若∠BAC=60°，
  ①求证：OD= $\text{[math]}$ OA.
  ②当OA=1时，求△ABC面积的最大值。
2. （2）点E在线段OA上，（OE=OD.连接DE，设∠ABC=m∠OED.∠ACB=n∠OED（m，n是正数）.若∠ABC<∠ACB，求证：m-n+2=0.
答案解析收藏纠错 + 选题
19. (2019·宁波) 如图1， $\text{[math]}$ O经过等边△ABC的顶点A，C（圆心O在△ABC内），分别与AB，CB的延长线交于点D，E，连结DE，BF⊥EC交AE于点F.
1. （1）求证：BD=BE.
2. （2）当AF：EF=3：2，AC=6时，求AE的长。
3. （3）设 $\text{[math]}$ =x，tan∠DAE=y.
  ①求y关于x的函数表达式；
  
  ②如图2，连结OF，OB，若△AEC的面积是△OFB面积的10倍，求y的值
答案解析收藏纠错 + 选题
20. (2019·湖州) 已知在平面直角坐标系xOy中，直线l₁分别交x轴和y轴于点A(-3，0)，B(0，3).
1. （1）如图1，已知⊙P经过点O，且与直线l1相切于点B，求⊙P的直径长；
2. （2）如图2，已知直线l₂： y＝3x-3分别交x轴和y轴于点C和点D，点Q是直线l₂上的一个动点，以Q为圆心， $\text{[math]}$ 为半径画圆.
  ①当点Q与点C重合时，求证：直线l₁与⊙Q相切；
  
  ②设⊙Q与直线l₁相交于M，N两点，连结QM，QN. 问：是否存在这样的点Q，使得△QMN是等腰直角三角形，若存在，求出点Q的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
21. (2019·柳州) 如图，AB是⊙O的直径，弦CD⊥AB于点E，点F是⊙O上一点，且，连接FB，FD，FD交AB于点N.
1. （1）若AE=1，CD=6，求⊙O的半径；
2. （2）求证：△BNF为等腰三角形；
3. （3）连接FC并延长，交BA的延长线于点P，过点D作⊙O的切线，交BA的延长线于点M.求证：ON·OP=OE·OM.
答案解析收藏纠错 + 选题
22. (2019·南通) 如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=1，以边AC上一点O为圆心，OA为半径的⊙O经过点B.
1. （1）求⊙O的半径；
2. （2）点P为 $\text{[math]}$ 中点，作PQ⊥AC，垂足为Q，求OQ的长；
3. （3）在(2)的条件下，连接PC，求tan∠PCA的值.
答案解析收藏纠错 + 选题
23. (2019·随州) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的⊙ $\text{[math]}$ 分别交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是⊙ $\text{[math]}$ 的切线；
2. （2）若⊙ $\text{[math]}$ 的直径为3， $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
24. (2019·辽阳) 如图， $\text{[math]}$ 是⊙ $\text{[math]}$ 的直径，点 $\text{[math]}$ 和点 $\text{[math]}$ 是⊙ $\text{[math]}$ 上的两点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作射线交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，使 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是⊙ $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ，求阴影部分的面积.
答案解析收藏纠错 + 选题
25. (2019·荆州) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点 $\text{[math]}$ 为 $\text{[math]}$ 上一点，点 $\text{[math]}$ 是半径 $\text{[math]}$ 上一动点（不与 $\text{[math]}$ ， $\text{[math]}$ 重合），过点 $\text{[math]}$ 作射线 $\text{[math]}$ ，分别交弦 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 两点，在射线 $\text{[math]}$ 上取点 $\text{[math]}$ ，使 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）当点 $\text{[math]}$ 是 $\text{[math]}$ 的中点时，
  ①若 $\text{[math]}$ ，判断以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是什么特殊四边形，并说明理由；
  
  ②若 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
26. (2019·大连) 如图1，四边形 $\text{[math]}$ 内接于圆 $\text{[math]}$ ， $\text{[math]}$ 是圆 $\text{[math]}$ 的直径，过点 $\text{[math]}$ 的切线与 $\text{[math]}$ 的延长线相交于点 $\text{[math]}$ .且 $\text{[math]}$
1. （1）求证： $\text{[math]}$ ；
2. （2）过图1中的点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ （如图2），当 $\text{[math]}$ ， $\text{[math]}$ 时，求圆 $\text{[math]}$ 的半径.
答案解析收藏纠错 + 选题
27. (2019·云南) 如图，AB是⊙C的直径，M、D两点在AB的延长线上，E是⊙C上的点，且DE²＝DB· DA.延长AE至F，使AE＝EF，设BF＝10，cos∠BED= $\text{[math]}$ .
1. （1）求证：△DEB∽△DAE；
2. （2）求DA，DE的长；
3. （3）若点F在B、E、M三点确定的圆上，求MD的长.
答案解析收藏纠错 + 选题
28. (2019·本溪) 如图，点 $\text{[math]}$ 为正方形 $\text{[math]}$ 的对角线 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆，连接 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，求 $\text{[math]}$ 的半径和线段 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
29. (2019·哈尔滨) 已知：MN为⊙O的直径，OE为⊙O的半径，AB、CH是O的两条弦，AB⊥OE于点D，CH⊥MN于点K，连接HN、HE，HE与MN交于点P．
1. （1）如图1，若AB与CH交于点F，求证：∠HFB=2∠EHN；
2. （2）如图2，连接ME、OA，OA与ME交于点Q，若0A⊥ME，∠EON=4∠CHN，求证：MP=AB；
3. （3）如图3，在（2）的条件下，连接OC、BC、AH，OC与EH交于点G，AH与MN交于点R，连接RG，若HK：ME=2：3，BC= $\text{[math]}$ ，求RG的长．
答案解析收藏纠错 + 选题
30. (2019·桂林) 如图，BM是以AB为直径的⊙O的切线，B为切点，BC平分∠ABM，弦CD交AB于点E，DE＝OE.
1. （1）求证：△ACB是等腰直角三角形；
2. （2）求证：OA²＝OE•DC：
3. （3）求tan∠ACD的值.
答案解析收藏纠错 + 选题
31. (2019·十堰) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的⊙ $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 延长线上一点，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是⊙ $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ，求⊙ $\text{[math]}$ 的半径.
答案解析收藏纠错 + 选题
32. (2019·江汉) 已知△ABC内接于⊙O ， ∠BAC的平分线交⊙O于点D ，连接DB ， DC ．
1. （1）如图①，当∠BAC =120°时，请直接写出线段AB ， AC ， AD之间满足的等量关系式：；
2. （2）如图②，当∠BAC =90°时，试探究线段AB ， AC ， AD之间满足的等量关系，并证明你的结论；
3. （3）如图③，若BC=5，BD=4，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
33. (2019·兰州) 主题学习
通过对下面数学模型的研究学习，解决（1）（2）题
【模型呈现】
如图，在Rt△ABC中，∠ACB=90°，将斜边AB绕点A顺时针旋转90°得到AD，过点D作DE⊥AC于点E，可以推理得到△ABC≌△DAE，进而得到AC=DE，BC=AE
我们把这个数学模型称为“K型”，
推理过程如下：

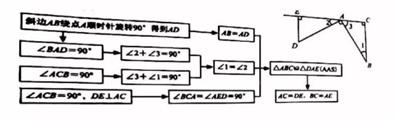
【模型应用】
如图，Rt△ABC内接于⊙O，∠ACB=90°，BC=2.将斜边AB绕点A顺时针旋转一定角度得到AD，过点D作DE⊥AC于点E，∠DAE=∠ABC，DE=1，连接DO交⊙O于点F.
1. （1）求证：AD是⊙O的切线；
2. （2）接FC交AB于点G，连接FB，求证：FG²=GO·GB.
答案解析收藏纠错 + 选题
34. (2019·黄石) 如图， $\text{[math]}$ 是⊙ $\text{[math]}$ 的直径，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上， $\text{[math]}$ 、 $\text{[math]}$ 是⊙ $\text{[math]}$ 上的两点， $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$
1. （1）求证： $\text{[math]}$ 是⊙ $\text{[math]}$ 的切线；
2. （2）求证： $\text{[math]}$
3. （3）若 $\text{[math]}$ ， $\text{[math]}$ ，求弦 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
35. (2018·株洲) 如图，已知AB为⊙O的直径，AB=8，点C和点D是⊙O上关于直线AB对称的两个点，连接OC、AC，且∠BOC＜90°，直线BC和直线AD相交于点E，过点C作直线CG与线段AB的延长线相交于点F，与直线AD相交于点G，且∠GAF＝∠GCE
1. （1）求证：直线CG为⊙O的切线；
2. （2）若点H为线段OB上一点，连接CH，满足CB＝CH，
  ①△CBH∽△OBC
  ②求OH＋HC的最大值
答案解析收藏纠错 + 选题
36. (2018·桂林) 如图1，已知⊙O是ΔADB的外接圆，∠ADB的平分线DC交AB于点M，交⊙O于点C，连接AC，BC.
1. （1）求证：AC=BC；
2. （2）如图2，在图1 的基础上做⊙O的直径CF交AB于点E，连接AF，过点A作⊙O的切线AH，若AH//BC，求∠ACF的度数；
3. （3）在（2）的条件下，若ΔABD的面积为 $\text{[math]}$ ，ΔABD与ΔABC的面积比为2：9，求CD的长.
答案解析收藏纠错 + 选题
37. (2018·广东) 如图，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接AC，OD交于点E．
1. （1）证明：OD∥BC；
2. （2）若tan∠ABC=2，证明：DA与⊙O相切；
3. （3）在（2）条件下，连接BD交于⊙O于点F，连接EF，若BC=1，求EF的长．
答案解析收藏纠错 + 选题
38. (2018·梧州) 如图，AB 是⊙M 的直径，BC 是⊙M 的切线，切点为 B，C 是 BC 上（除 B 点外）的任意一点，连接 CM 交⊙M 于点 G，过点 C 作 DC⊥BC 交 BG 的延长线于点 D，连接 AG 并延长交 BC 于点 E．
1. （1）求证：△ABE∽△BCD；
2. （2）若 MB=BE=1，求 CD 的长度．
答案解析收藏纠错 + 选题
39. (2018·贵阳) 如图，AB为⊙O的直径，且AB=4，点C在半圆上，OC⊥AB，垂足为点O，P为半圆上任意一点，过P点作PE⊥OC于点E，设△OPE的内心为M，连接OM、PM．
1. （1）求∠OMP的度数；
2. （2）当点P在半圆上从点B运动到点A时，求内心M所经过的路径长．
答案解析收藏纠错 + 选题
40. (2018·德阳) 如图，在直角三角形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的内心， $\text{[math]}$ 的延长线和三角形 $\text{[math]}$ 的外接圆 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连结 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线交 $\text{[math]}$ 、 $\text{[math]}$ 的延长线分别于点 $\text{[math]}$ 、 $\text{[math]}$ ，已知 $\text{[math]}$ ，圆 $\text{[math]}$ 的直径为 $\text{[math]}$ ，①求证： $\text{[math]}$ 为圆 $\text{[math]}$ 的切线；②求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题